John D. McCalpin, Ph.D., informally known as “Dr. Bandwidth” for his invention of STREAM memory bandwidth benchmark, posted STREAM results for Intel Xeon Phi and two Xeon-based servers made by Dell (see the end of his blog entry). All three devices are used in the “Stampede” computer at TACC.
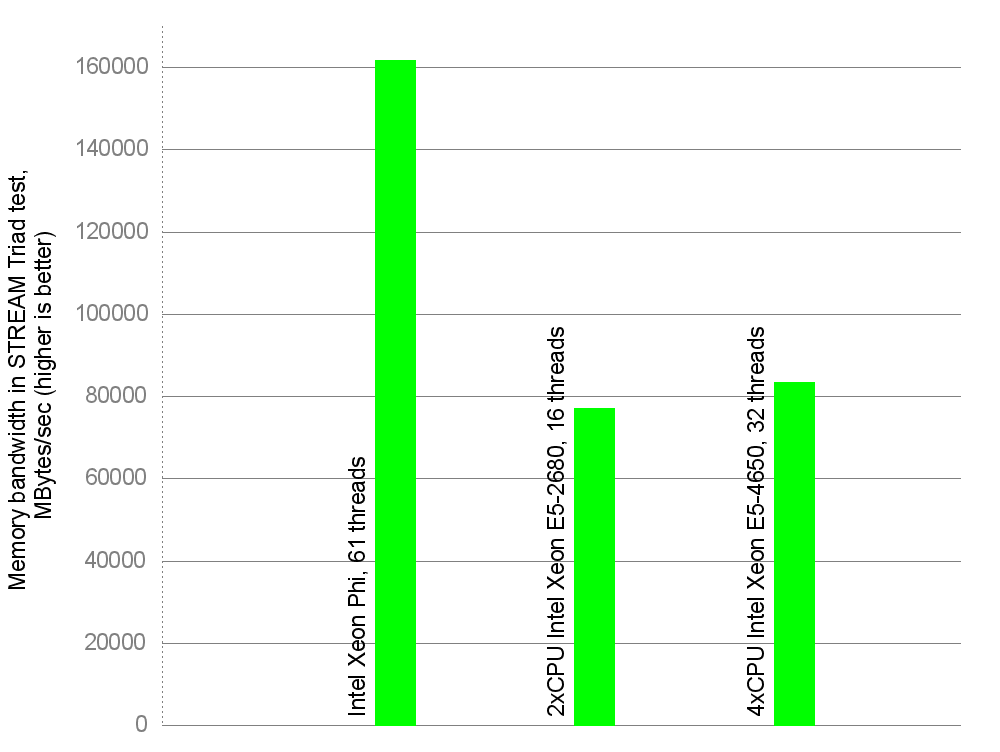
Intel Xeon Phi achieved memory bandwidth of roughly 161829 MBytes/second — not bad, to say the least! It is this product that I called “monstrous” 6 months ago. I decided to turn the numbers into a graphical form. Also present on the graphs are results of the aforementioned 2xCPU and 4xCPU Intel Xeon-based servers used as compute nodes in “Stampede”. First, total memory bandwidth per device: per Xeon Phi board, or per Xeon-based server:
In this test, the number of OpenMP threads used by STREAM was equal to the number of cores on the computing device. As can be seen, Intel Xeon Phi board supplies a lot of bandwidth to its cores. The hi-end dual-socket and quad-socket servers are lagging behind in total bandwidth, and the quad-socket server is only marginally better than its dual-socket peer.
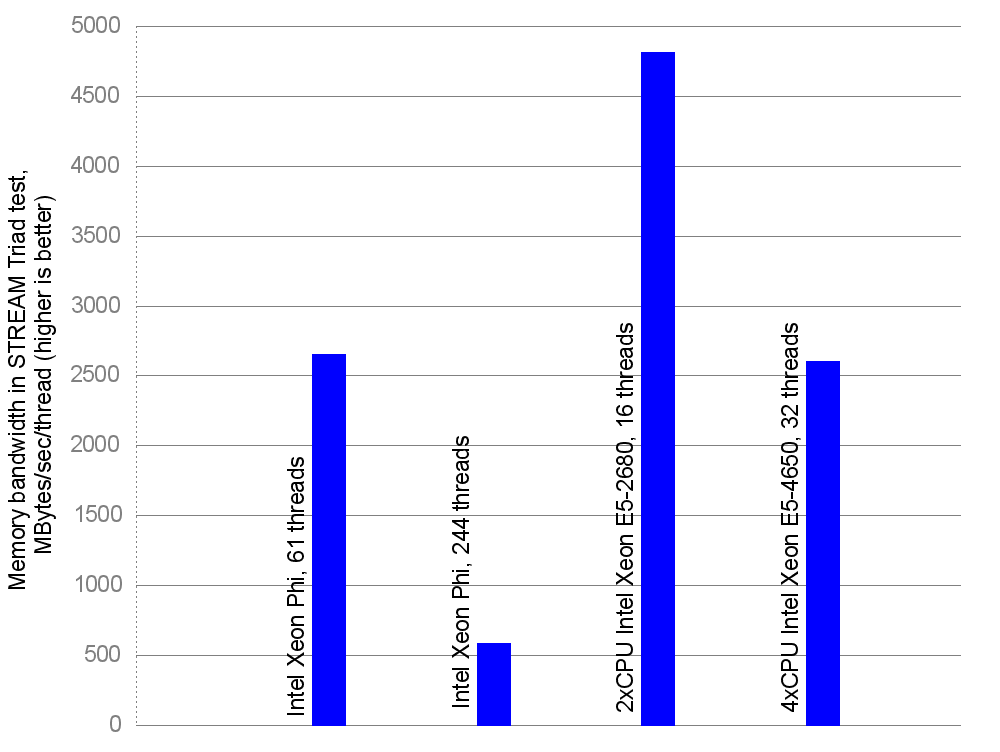
Now, let us divide the total bandwidth by the number of threads running on the computing device, in order to understand how much bandwidth one thread can receive:
This graph features two bars for Intel Xeon Phi. The reason is that to fully utilize Xeon Phi’s floating-point capabilities, you often need to spawn 4 threads per each of its cores (but see also Update 1 at the end of the post). Here’s the quote from a paper by James Reinders of Intel:
The Intel Xeon Phi coprocessor offers four hardware threads per core with sufficient memory capabilities and floating-point capabilities to make it generally impossible for a single thread per core to approach either limit. Highly tuned kernels of code may reach saturation with two threads, but generally applications need a minimum of three or four active threads per core to access all that the coprocessor can offer.
That’s why the realistic usage scenario for floating-point-limited applications would involve 61*4=244 threads. But STREAM run with 244 threads shows 12% less total bandwidth than with 61 threads:
6. The best results with the compiler flags above were obtained with one thread per core. Using 2, 3, or 4 threads per core decreased the Triad bandwidth by approximately 4%, 8%, and 12%, respectively.
Therefore the second bar for Intel Xeon Phi is so much lower. The dual-socket server now is the best of all with regard to bandwidth per thread.
It should be noted, however, that STREAM was designed to measure one specific thing — memory bandwidth, and therefore it “emulates” only one sort of applications: those that read immense amounts of memory, word by word, do a few floating-point operations on them, and write the results back. There are other types of memory access patterns: for example, when the working set of a program fits in cache memory, and there are many iterative floating-point operations over the same data, then memory bandwidth is less important. Therefore the outlooks are not so bleak for Intel Xeon Phi!
This second graph, although providing more insight than the first one, still doesn’t complete the picture. That’s because we didn’t take into account floating-point capabilities of the devices. Intel Xeon Phi has a lower clock frequency, but can do more floating-point operations per each clock cycle.
Let us calculate peak floating-point rates for the devices. For Intel Xeon Phi, there is the following quote on the product page:
2. Claim based on calculated theoretical peak double precision performance capability for a single coprocessor. 16 DP FLOPS/clock/core * 60 cores * 1.053GHz = 1.0108 TeraFlop/s.
How did they arrive to 16 FLOPS/cycle? The SIMD unit within the core is 512 bits wide, so it can hold 8 double-precision (64 bit) floating-point numbers. Xeon Phi supports fused multiply-add (FMA) instructions, where one single instruction performs one multiply and one add operations, totalling two floating-point operations, such as d ← d * a + b (take contents of register d, multiply it by a, add b, and save the result back to d). See, for example, instruction VFMADD132PD (or similar ones) from this instruction set architecture reference manual (page 201 of 725). This presentation by George Chrysos of Intel affirms this. So, each cycle 2 floating-point operations are performed on 8 numbers, which results in 2*8=16 FLOPS/cycle.
Therefore, if your code does one multiplication and one addition (and not two additions, or two multiplications, or anything else) with long floating-point vectors, then you have a chance to approach that peak performance.
Now, we need to calculate the peak floating-point rate for dual-socket and quad-socket Dell servers, which are based on Intel Xeon E5-2680 and Xeon E5-4650 processors, respectively (both are 8-core, 2.7 GHz). Both CPUs support advanced vector extensions (AVX). The vector units are 256 bits wide, so they can hold 4 double-precision floating-point numbers. Using the same reporting methodology with FMA instructions as above, in one cycle you can achieve 4 additions and 4 multiplications, for a total of 8 FLOPS/cycle. We then need to multiply this by the clock frequency of 2,7 GHz, by 8 cores, and by the number of sockets. This gives 345,6 GFLOPS for the dual-socket server, and 691,2 GFLOPS for the quad-socket one.
Finally, we know the total memory bandwidth per device, and the peak floating-point rate per device. There is a metric called machine balance. It tries to convolve all intricate parameters of parallel computers, many of which have non-linear relation to performance, into one single number. Of course, it cannot be precise. But it allows for rough comparisons between architectures. To calculate machine balance, you need to divide the peak floating-point rate, in GFLOPS, by the total memory bandwidth, in GWords/sec.
The result is measured in FLOPs/Word and, most simply put, it indicates how many floating-point operations your computer can perform with each word that arrived from memory before the next word comes in for processing. Yes, it is a big simplification. High numbers (for example, 30 FLOPs/Word) are a bad sign, they indicate unbalanced machines: that is, for every word that arrives, the machine can perform 30 floating-point operations before the next word arrives. And what happens if your code just doesn’t need to perform 30 floating-point operations on the single word that came in from memory? Then the CPU has to stay idle, doing no useful work, until the next word comes in, because memory is too slow for this CPU, and therefore the machine is called “unbalanced”. (Again, it’s a very rough approximation of how computers work, because it’s not a single word that is fetched from memory at a time, but a whole cache line, etc., etc.)
Many of today’s machines are unbalanced in this respect, compared to vector supercomputers of the good old days. Cache memories in modern machines try to alleviate this problem. So, let us calculate machine balance for the three computing devices. There will be three bars on the graph for Intel Xeon Phi — for 61 threads (1 thread per core), for 122 threads (2 threads per core), and for 244 threads (4 threads per core).
Note that “a thread can only issue a vector instruction every other cycle”, therefore you need at least two threads to reach the maximum instruction issue rate. Additionally, “using 3-4 threads does not increase maximum issue rate, but often helps tolerate latency” (ibid, slide 15 of 26).
Therefore, to fully exploit the floating-point capability of Intel Xeon Phi, you are likely to use 2 or 4 threads per core, resulting in 122 or 244 threads per device, but to allow for more memory bandwidth for bandwidth-limited applications, you can try 1 thread per core. (See also Update 1 at the end of the post).
Intel Xeon Phi.
244 threads: total bandwidth with 244 threads: 142410 MB/sec (161829 minus 12%), or 17,8 GWords/sec. Peak floating-point rate with 61 cores: 16 DP FLOPS/cycle/core * 61 cores * 1,053 GHz = 1027,7 GFLOPS. Machine balance: 57,7 FLOPS/Word.
122 threads: total bandwidth with 122 threads: 155356 MB/sec (161829 minus 4%), or 19,4 GWords/sec. Peak floating-point rate: same. Machine balance: 53 FLOPS/Word.
61 threads: total bandwidth with 61 threads: 161829 MB/sec, or 20,2 GWords/sec. Peak floating-point rate: half of the above peak, that is, 513,9 GFLOPS, because, as noted above, “a thread can only issue a vector instruction every other cycle”. Machine balance: 25,4 FLOPS/Word.
Dual-socket Intel Xeon-based server. Total bandwidth: 77010 MB/sec, or 9,6 GWords/sec. Peak floating-point rate: 345,6 GFLOPS (see above). Machine balance: 36 FLOPS/Word.
Quad-socket Intel Xeon-based server. Total bandwidth: 83381 MB/sec, or 10,4 GWords/sec. Peak floating-point performance: 691,2 GFLOPS (see above). Machine balance: 66,5 FLOPS/Word.
Here is the corresponding graph (remember: lower is better!):
Don’t forget that these balance figures were calculated from STREAM Triad results which, as you remember, emulate only one memory access pattern. If your code is cache-friendly, you will benefit from cache memory bandwidth, which for Intel Xeon Phi is 7 and 15 times higher than main memory bandwidth, for L2 and L1 caches, respectively (see Figure 14 in this presentation).
Note also this blog post by Dr. McCalpin, where he, among other things, compares machine balance of Intel Xeon Phi to that of NVIDIA’a GPU accelerators.
Thanks for reading this far! To download source data for the graphs for plotting with Gnuplot, click here.
Update 1. Dr. McCalpin wrote me by e-mail that there are, in fact, applications that run faster when they use 1, 2 or 3 threads per Xeon Phi core, instead of the maximum number of 4 threads per core.