Colfax International is a US-based IT equipment and solution provider. What’s so special about them is that their web-based retail shop, Colfax Direct, lists thousands of items ready to be shipped, and all prices are available online, with no dumb “request a free quote” buttons or whatever.
Another nice feature of Colfax International is that they have a real, customer-facing research division, which is also uncommon among solution providers. In January 2013, Andrey Vladimirov of Stanford University and Vadim Karpusenko of Colfax International conducted some testing of the then-new Intel Xeon Phi coprocessors on the N-body problem, summarising their results in an article.
The N-body problem considers interaction of a large number of objects affected by gravitational forces, and is widely used in astronomy. The above-mentioned article describes a couple of coding optimisations that allow to significantly speed up computations, but you should better take a look at the animation below which says it all. The idea is that with more Intel Xeon Phi coprocessors you can calculate a longer sequence of particle interactions in a given time. And you do want to have a fast machine to calculate such things for you if you have an asteroid moving on a collision course with the Earth and which you intend to break up into parts.
What interested me in the video is the graph with performance results of N-body simulation on a server equipped with up to eight Intel Xeon Phi coprocessors (see the screenshot below, made at 1:00 into the video).
This performance data is valuable, but we can make it even more valuable if we compound it with equipment costs.
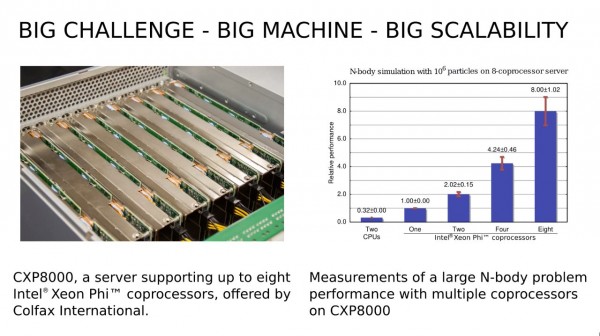
Performance results for N-body simulation for servers with zero to eight Intel Xeon Phi coprocessors. Data gathered by Andrey Vladimirov of Stanford University and Vadim Karpusenko of Colfax International.
To calculate costs, I used the configurator for the CXP9100 server available on the website. Let the baseline configuration be as follows:
Primary and secondary CPUs: Intel Xeon E5-2680
RAM: 2×16 GBytes Registered ECC DDR3; 32 GBytes total
Interconnect: Dual port Mellanox InfiniBand FDR module
This baseline configuration costs $10,706. Let us assume we use Intel Xeon Phi coprocessor model 5110P, each board costs $3,047 at Colfax International (the recommended customer price from Intel is $2,649). I summarised five configurations, together with their cost and performance figures, in this table:
| Configuration ID | No. of coprocessors | Relative performance | Cost ($) | Cost/Performance |
| 1 | 0 | 0,32 | 10706 | 33456 |
| 2 | 1 | 1,00 | 13753 | 13753 |
| 3 | 2 | 2,02 | 16801 | 8317 |
| 4 | 4 | 4,24 | 22896 | 5400 |
| 5 | 8 | 8,00 | 35086 | 4386 |
The lower the cost/performance ratio, the better. In this table, the lowest value is observed for the last configuration with 8 coprocessors.
For me, this was a bit surprising. This happened because this code has linear scalability: the configuration with 8 coprocessors is exactly 8 times faster than the configuration with only one coprocessor (and it was surprising for me because I failed to notice linear scalability from the start).
The reason for this behaviour is that the task to be solved is large enough (N=106 particles), so time in the system is mostly spent on number-crunching, and overheads such as initialisation and network communication are negligible. (As a conversation with the research team revealed, performance figures from the graph do include all overheads, but these are small enough and do not affect linear scaling; see update below).
Scaling ceases to remain linear when the overall performance of the task becomes bound by some subsystem of the computer, usually memory, network or disk. In our case, scaling remains linear, which means that the task just didn’t stress memory and network high enough (in this case, the network that connects coprocessors together is the PCIe interconnect on the server motherboard).
For most tasks, adding more and more processing elements sooner or later starts to yield less and less benefits, and performance “flattens out”. If this were the case in our example, having just two or four coprocessors per server could very well be the “sweet spot”, characterised by the lowest value of the cost/performance ratio.
For those of you who have read this far, let me reveal what were the optimisations described in the research paper by Andrey and Vadim. The first one was memory fetching optimisation, ensuring so-called unit stride access to array elements. This helps to better use caches, and immediately gave a 3,4x speedup for Intel Xeon Phi.
The other optimisation is more subtle but also more interesting: the researchers noticed that the single square root operation takes up suspiciously much time. By using a compiler flag, they replaced it with the lower-precision version which executes much faster (ensuring, of course, that it doesn’t hurt the solution), and this small but unobvious change gave a further 2,1x speedup.
Thanks for reading, and now you know the way to calculate the optimal number of coprocessors per server: fill out the table above and find the row where the cost/performance ratio is minimal; this will be your optimal configuration.
UPDATE: A comment by Andrey Vladimirov further explains why linear scaling can be observed in this and several other important cases:
I definitely agree that, as you say, application scaling usually becomes non-linear at some point, and if it happens before 8 coprocessors per system, then the most “loaded” configuration may not be the “sweet spot”.
However, with regards to the N-body problem, the performance is really linear up to 8 coprocessors, and chart in the video shows true timing, with initialization, data transfer, load imbalance, and everything else included. The reasons for linear scaling are, first, that we chose a large enough problem and, second, that in our algorithm, the arithmetic workload scales as O(N²), and the data transfer time scales as O(N).
In the world of N-body simulations, our demo is a “toy model”. For more efficient N-body simulations suited for a huge number of particles, achieving linear scaling may be more tricky.
At the same time, there are a lot of problems out there that are just like our demo (such as the common dense matrix multiplication and inversion) and also problems with “embarrassingly parallel” codes (such as all kinds of map-reduce type of operations).
For these, linear scalability across 8 coprocessors is quite realistic, and we wanted to demonstrate just that.
